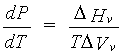
| Simulated materials have finite molecular weight |
| Peter H. Nelson |
| Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge Massachusetts 02139 |
| (submitted to the Journal of Chemical Physics, May 1996) |
| The thermodynamic molecular weight of any entity in an atomistic simulation is limited by the size of a single periodic image. This can cause significant finite-size effects in small-scale simulations of materials, such as polymers, whose phase behavior depends strongly on molecular weight. A method is proposed to formally increase the molecular weight of the material, without computational overhead, within the rigid approximation. |
I. INTRODUCTION.
It is well-known that small molecules have significantly different properties from polymers. For example, consider the difference between alkanes and polyethylene. What does not appear to have been widely appreciated is that simulations of materials, such as polymers, have a finite-size effect which is equivalent to assigning a molecular weight equal to that of a single periodic image in the simulation. From a thermodynamic point of view, connection of a polymer to itself across a periodic boundary does not increase its molecular weight at all!
As an example, consider a simulation of an endless polymeric substance which has two ethylene repeat units. It is contended that this simulation should be thought of as a topologically constrained form of endless C2H4 rather than high molecular weight polyethylene. Hence, based on the properties of ethane at room temperature and pressure, this system is expected1 to be a low density fluid close to its critical temperature, whereas at room temperature polyethylene is a solid with an extremely low vapor pressure.
This is simply a finite-size effect.
The effect is large for low molecular weight polymeric systems
because high molecular weights are required for alkanes to behave
like polyethylene, for example.
II. THERMODYNAMIC MOLECULAR WEIGHT
The Clausius-Clapeyron equation relates the pressure P and the temperature T along a phase boundary in the P-T plane. For example, consider the liquid-vapor coexistence curve:
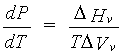
where DHv is the enthalpy of vaporization and DVv is the volume change upon vaporization. (Note, a similar analysis can be made for the solid-vapor coexistence curve.) At low pressures, DVv may be approximated by RT/P, assuming ideal gas behavior. For short alkanes1, DHv~NQ, where N is proportional to the (thermodynamic) molecular weight of the alkane, and Q is independent of molecular weight. This illustrates the connection between molecular weight and phase behavior, as DHv has a strong dependence on molecular weight and DVv is independent of it (within the low-pressure ideal gas approximation).
The ideal gas approximation becomes a good one for high molecular weight polymers as the vapor pressure (at room temperature) becomes extremely low. The approximation for the enthalpy change can be replaced with DHv~N2/3hs, in this limit, where hs is related to the surface enthalpy of the polymeric liquid and is assumed to be independent of N. This expression is based on the prediction that collapsed coils2 are expected in the gas phase, which can be modelled as liquid drops from an enthalpic point of view. Hence, for large N, the Clausius-Clapeyron equation may be approximated by:
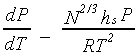
This slope also has a strong dependence on molecular weight. For the solid-liquid coexistence curve, both DHm and DVm (for melting) are expected to have a linear dependence on N. These will cancel each other out to give a liquid-solid coexistence curve whose slope is independent of molecular weight in the high molecular weight limit.
It should be noted that the Clausius-Clapeyron
equation is not applicable to the vibrational analyses of infinite
crystalline lattices3. Phase changes are not possible,
which is equivalent to assigning an infinite thermodynamic molecular
weight to this type of calculation. This highlights an under-appreciated
advantage of such calculations over atomistic simulations of crystalline
polymeric materials at low pressure. In light of the above, it
is worthwhile carefully reviewing some of the salient aspects
of using periodic boundary conditions.
Periodic boundary conditions
These are a well established method
of removing surface effects in computer simulations4.
This is done by connecting the edges of the simulation space in
a manner similar to some video games: if something moves off the
right hand side it arrives on the left hand side, as if the two
sides were connected seamlessly together. In two dimensional simulations,
the left- and right-hand edges are connected together in this
way, as are the top and bottom edges of the simulation space.
This is often illustrated as a central simulation box surrounded
by periodic images of itself (Fig. 1). This creates what appears
to be an infinite lattice. Conceptually, the effects of long range
interactions can be accounted for by the use of this type of picture,
but the periodic images just are a convenient fiction for easily
visualizing the longer range behavior and interactions. In polymeric
systems, the periodic boundaries can be further used to remove
the ends of the polymers (Fig. 1), if desired. It is useful to
think of the monomers as being part of infinite polymers from
a topological point of view, but the polymers still have a finite
thermodynamic molecular weight.
|
III. PARALLEL RIGID RODS
Consider a system of rigid rods of length l, whose axes are all rigidly aligned in the z-direction, and which are constrained not to move in the z-direction. This system can be mapped onto the well-studied 2d Lennard-Jones system4 (for example) by assigning a pair-wise interaction, per unit length, between pairs of rods so that erod=le/s, and assigning unit mass per unit length of the rod so that mrod=lm/s, where s, e and m are the Lennard-Jones parameters. This rod system is identical to the 2d system when l=s, otherwise, the system corresponds to the 2d system with scaled quantities T=iT1 and P=iP1. Where i=l/s, and T1 and P1 are the values for the i=1 system. Thus, the P-T phase diagram of the rod system is obtained by a simple enlargement proportional to molecular weight. Note, the dimensionless quantities for the rods are T*=kT/(ie) and P*=Ps3/(ie).
There are no end effects for the rods so we can apply periodic boundary conditions along the z-direction without altering the physics of the system. This allows the rigid rods to be used as a simple model of polyethylene. An estimate of e»2.3kJ/mol and s»2.8A can be made by comparing the estimated3 lattice energy and density of zero temperature polyethylene with the rigid rod system5 at a density of r*=0.9165. Using these values we can investigate the effects of finite molecular weight on simulations of "polyethylene" of arbitrary molecular weight. The (i=2)-system, which is simulated at room temperature (T*»0.54) and at the density of bulk polyethylene (r*»0.92), is a solid close to its critical temperature (TC*=0.533). Note that the critical temperature of ethane is 305K. This close agreement is somewhat fortuitous.
An easily measured indication
that the i=2 simulation suffers from significant finite-size
effects is that the pressure is very high P»1GPa,
due to the compression required to maintain the supercritical
material at solid densities. At atmospheric pressure (P*»0.0003),
and at room temperature the material is a low density fluid. Hence,
we have confirmed that simulations of materials with anisotropic
bonding (e.g. covalent in certain directions only) can suffer
from the predicted finite-size effects which are attributable
to finite thermodynamic molecular weight.
Replication index i
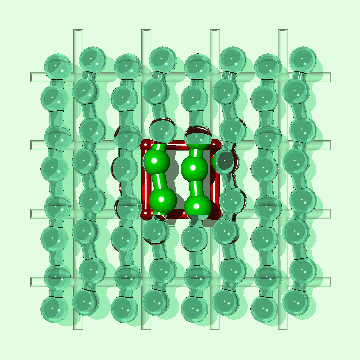
Simulation of an interfacial boundary also highlights the effect of molecular weight on the phase behavior of all simulated polymers, both rigid and flexible. The system shown in Fig. 2 is an endless material having a condensed phase in equilibrium with its own vapor. The enthalpy of vaporization DHv (for moving a single polymer from the condensed phase to an "isolated" position in the gas phase) will have a value of say Q (per polymer) for the single layer system. For a three layer system (Fig. 3) DHv»3Q. This is the same relationship which is exact for the rigid rod model and an approximation for real alkanes. Whether a polymer is flexible or has end groups does not affect the first-order approximation that the enthalpy change is proportional to molecular weight.
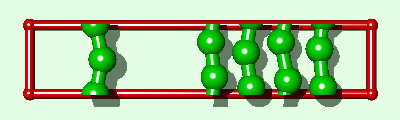
|
The difference between the single layer system (Fig. 2) and the three layer system (Fig. 3) is the length of the simulated polymer. Hence, if we explicitly replicate the one layer system three times (Fig. 4), where all three copies move in lock-step with each other, we obtain a system which is comparable to the three layer system, from a thermodynamic point of view, within the rigid approximation. The replicas represent a physical enlargement of the simulation box and should not be confused with periodic images of the simulated system (now three times bigger) which are also present conceptually. In determining how to simulate such a replicated system, it must be recalled that the simulated system is now i-times bigger than the unreplicated system. For example, in standard microcanonical ensemble molecular dynamics calculations4, the mass of each particle, and the forces, should be multiplied by the replication index. This does not alter the dynamics of the simulated system but it does alter the calculation of some of the thermodynamic quantities of interest. For example, in a replicated 3d Lennard-Jones system the dimensionless quantities are T*=kT/(ie), and P*=Ps3/(ie).
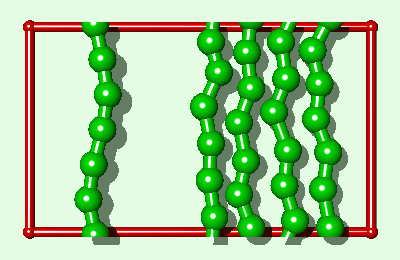
|
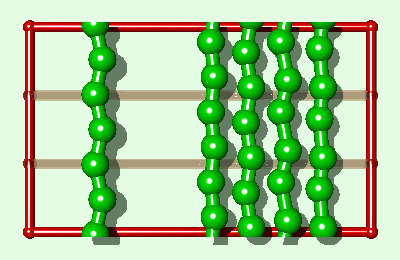
|
When calculating energy differences in a Monte Carlo scheme, using Metropolis sampling4, the energy difference calculation should be multiplied by the replication index before being used for an acceptance criterion. In canonical ensemble calculations, the energy differences are used in a form DE/kT, this should be modified to iDE/kT for a system replicated i times. This is another form of the temperature rescaling characterized by the replication index. The physical basis for the Monte Carlo replication method is that the random heat baths in the replicated copies are assumed to be statistically independent of each other, despite the fact that the replicated copies molecules move in lockstep. This means that replicated Brownian-dynamics simulations (or any other type of simulation method using a fictitious heat bath) should also be possible.
Unfortunately, the replication
mechanism, while being an exact approximation for rigid systems,
is of limited applicability to simulations of more realistic flexible
systems. For example, in the rigid rod system, the melting temperature
at low pressures (P*_0.1) is approximately equal to Tt*,
the triple point temperature. This is consistent with the observation
that the melting points of C3H8 to C8H18
are approximately proportional to molecular weight (although the
numerical values are larger than experiment by factors of between
3.4 and 4.4). However, as the molecular weight of the alkanes
is increased further, the rigid approximation becomes increasingly
inappropriate and the melting points cease to be proportional
to molecular weight and approach the (constant) value of high
molecular weight polyethylene.
Other materials
Simulations of non-polymeric systems (e.g. silicon), have finite-size effects which generally produce "small-system" loops4. These finite-size effects do not include the significant changes in phase diagram structure predicted for polymers. This is because the only thermodynamically significant molecular weight in the simulation6 is the molecular weight of the atoms or molecules themselves.
However, non-polymeric materials
with more than one type of bonding can suffer from finite-size
effects which may drastically alter the phase diagram of the simulated
system. For example, consider that the planes of graphite can
be thought of as a 2d (planar) analog of 1d (linear) polymers.
Hence, the thermodynamic molecular weight of a plane of carbon
atoms in an atomistic simulation will affect the phase behavior
significantly. For a six-carbon plane, the phase diagram is expected
to more closely resemble an orientationally constrained form of
benzene ring, than graphite. For non-replicated systems, the finite-size
effects will become small as the infinite-size regime is approached
and bulk properties can be simulated. For graphite (just as for
polymers) this may be a high molecular weight due to the relatively
weak bonding between planes on a per-atom basis.
IV. SUMMARY
The thermodynamic molecular weight of any entity in an atomistic simulation is limited to the size of a single periodic image. This finite-size effect can be shown to affect the phase behavior of any simulated material by considering the Clausius-Clapeyron equation. These effects have been confirmed by considering simulations of the Lennard-Jones parallel rigid rod model for polyethylene. For simulations of low molecular weight the finite-size effects are large enough to shift the simulation into an undesired part of the phase diagram. The use of replication rescaling (which is an exact approximation for the rods) can be used to formally increase the molecular weight of any simulated system, without additional computational overhead, thus shifting the simulated system back into the desired part of the phase diagram. Unfortunately, this rescaling is of limited applicability to real polymers due to the unphysical rigid constraints that are imposed between replica copies. These rigid constraints are equivalent to multiplying the forces and atomic weights by the replication index to artificially increase the molecular weight.
The effect of low thermodynamic molecular weight on more realistic simulations can be readily confirmed by investigating the phase behavior of the simulated material as a function of system size. As we have seen, low thermodynamic molecular weight dramatically affects constant (atmospheric) pressure simulations as the simulated polymer will generally be fluid rather than solid at room temperature. At solid densities, the prediction is that the pressure will be significantly higher than atmospheric pressure. Comparison of the finite molecular weight simulations with the equivalent crystalline material of infinite thermodynamic molecular weight is possible using vibrational analyses (e.g. ref 3).
The ability of computer simulations
to predict macroscopic phase behavior, from microscopic potential
functions, has led to their widespread use. However, it is this
very same ability which produces finite-size effects caused by
finite molecular weight.
References
1. e.g. CRC Handbook of Chemistry and Physics, 76th Edition, edited by D. R. Lide and H. P. R. Frederikse, (CRC Press, Boca Raton, 1995-1996).
2. P. G. de Gennes, Scaling Concepts in Polymer Physics (Cornell University, Ithaca, 1979).
3. N. Karasawa, S. Dasgupta, W. A. Goddard III, J. Phys. Chem. 95, 2260 (1991).
4. e.g. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids (Oxford University Press, Oxford, 1987) and references therein.
5. Barker , Henderson, D. and Abraham F. F. Physica 106A, 226 (1981).
6. This is true under normal conditions,
but near the critical point clusters of atoms of arbitrary molecular
weight become thermodynamically significant.
The manuscript has now been peer reviewed. Click
here.
 go back
go back